CS231N Lec. 7 | Training Neural Networks II

26 Oct 2020 in Studies on Lecture-Review

please find lecture reference from here¹

CS231N Lec. 7 | Training Neural Networks II

Normalization

Normalization make your model less sensity for variations.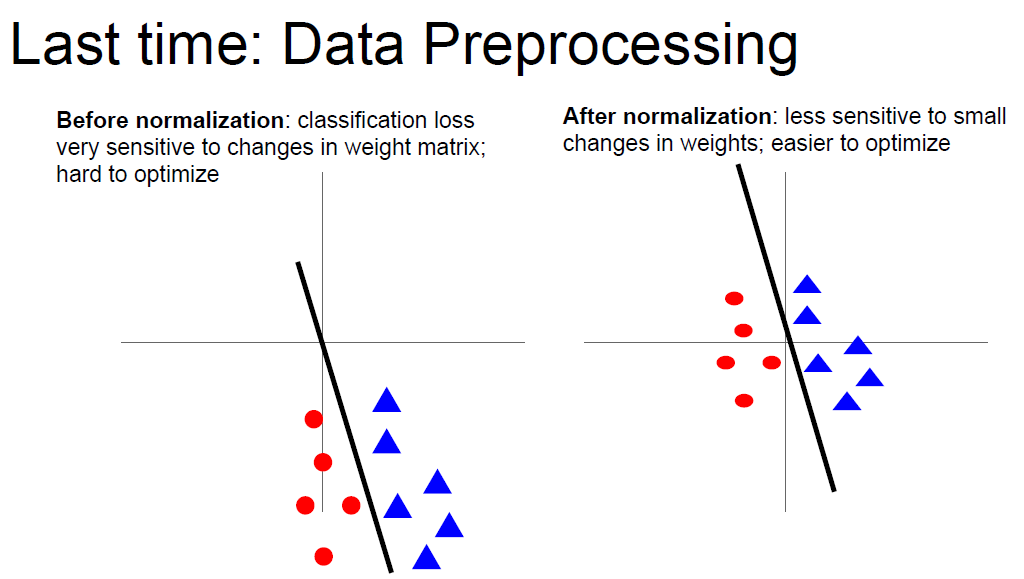

Problems with SGD

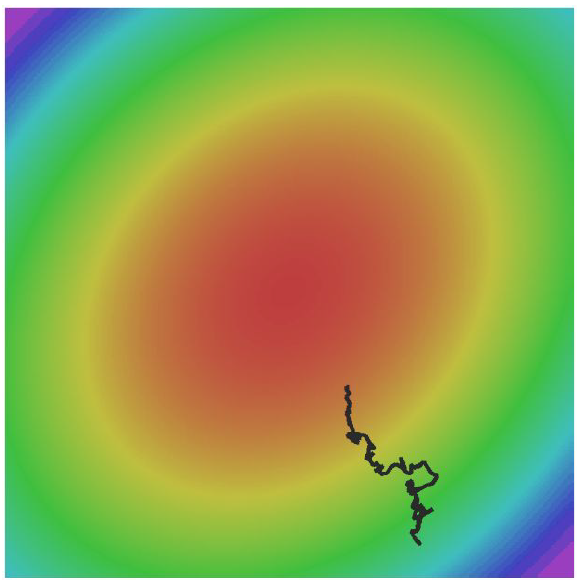
1. Sensitivity
   if loss change one direction very quickly and slowly in another, (in this case, quick for center, slow of circular) then, like below, we might troubled in inefficient learning. This could be much worse for multiple dimension.

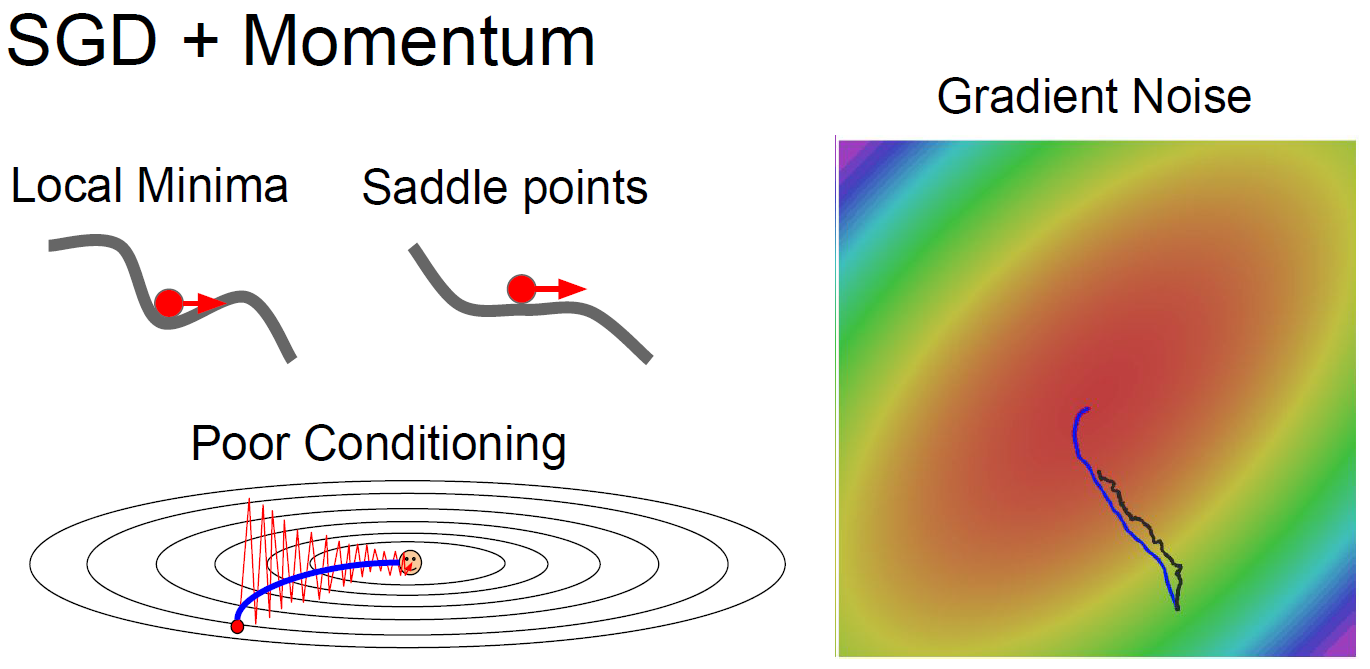
1. Local Minima and saddle point
   SGD can be stuck at local minima and saddle point(which is common for high-dimension).

e.g) one example for poor movement of SGD

Problem solving - Add Momentum

• Add tiny “momentum” to maintain movement.

Idea is quite simple, but result is very strong

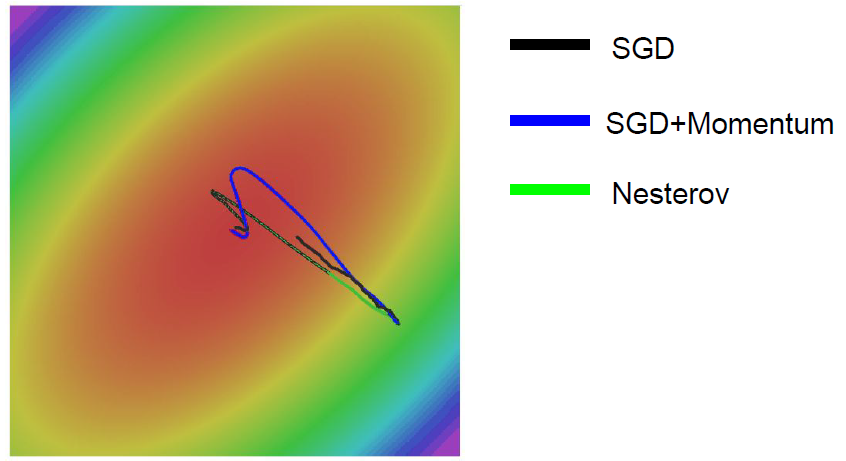
Nesterov Momentum

Kind of error fixing for previous velocity.

Why we learn annoying thing? because it’s effectvie…

Q. What if velocity is fast so, passing sharp minima?
A. Good question, actually we ignore that kind of sharp minima. Because, it’s kind of overfitting. So, If environment changed, sharp minima could be disappeared. In some sense, SGD+Momentum have a feature ignoring sharp minima.

AdaGrad

• Adding square of grad & divide root of this

This make slow make faster, fast make slower.

• Cons But if learning progress so far, step size becomes too small.

RMSProp

• Add decay rate for AdaGrad.

Adam (draft)

• Mix of Adagrad + RMSProp

• Problem We’ve initialized “second_moment” as 0, so at the 1st step “second_moment” should be very small, we divide by “second_moment” which is very small number, resulting x changed very large.

Adam (full form)

Adam full form fixed above problem of Adam (draft), by bias correction. Adam shows quite good performance for multiple models. Usually used for default algorithm.
Try use beta1 = 0.9 / beta2 = 0.999 / learning_rate = 1e-3 or 1e-5

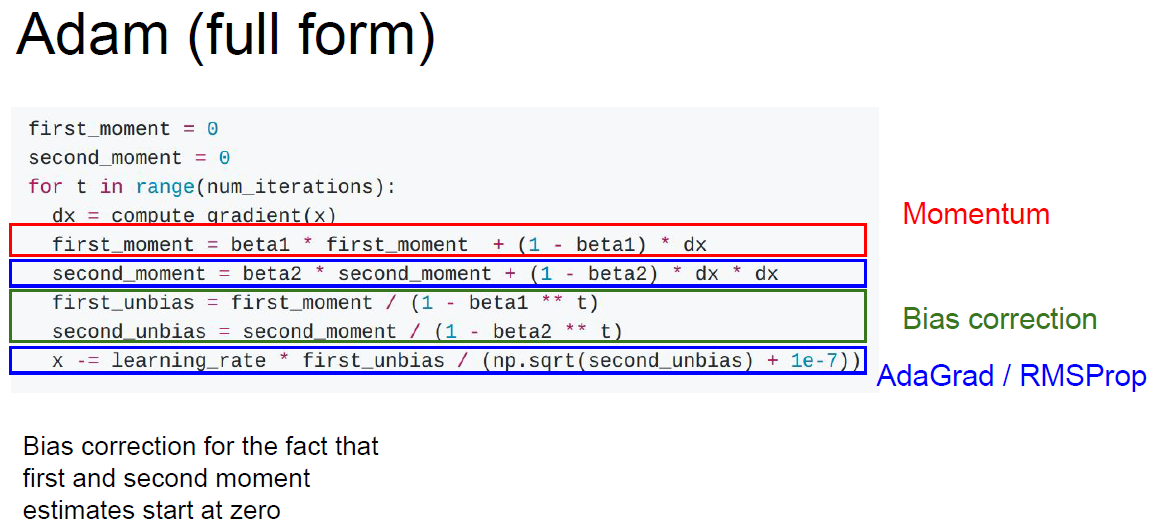
Q. What problem Adam still have?
A. If Oval tilted, than problem we observed at SGD, zigzaging, will be reproduced.

Learning rate decay

Exponential and 1/t decay exist. It’s common for SGD, less common with Adam.
Also, it’s secondary hyperparameter. you shouldn’t fit learning rate decay at first.

First-Order Optimization

We’ve talked about this algorithm.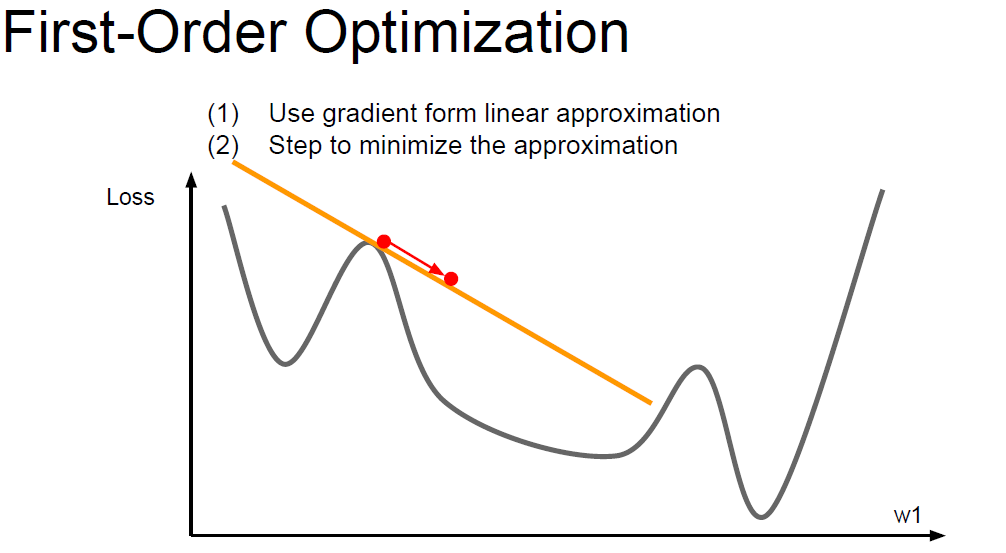

Second-Order Optimization

Little bit fancier.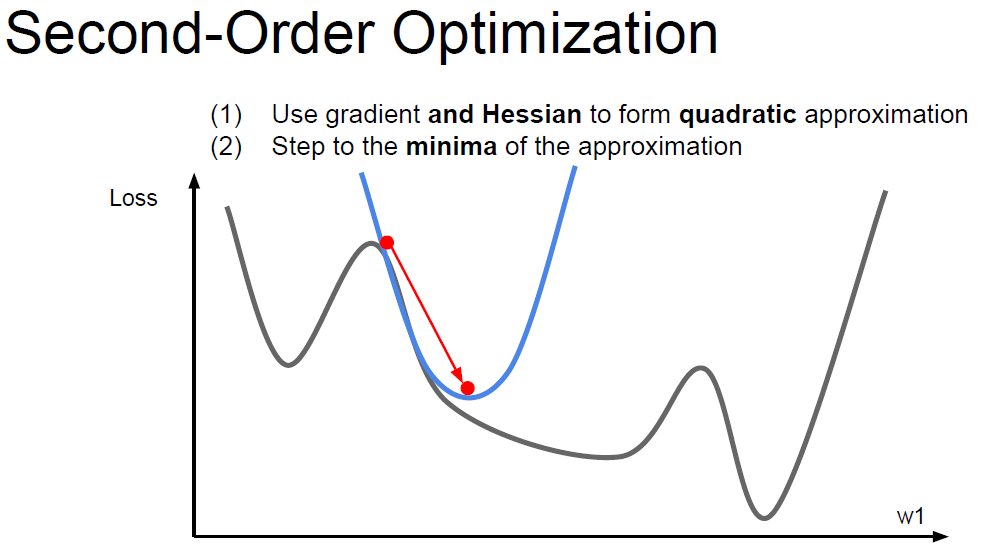

Q1. What is nice?
A2. It doesn’t have *Learning rate !.*
Because we could just calculate both dots. ( But only for vanila version )

Q2. Why is this bad for deep learning?
A2. Hessian has O(N^2) elements, inverting takes O(N^3) which is quite expensive. So, in practical, people use approximation.

In practice :

• Adam for good default option.
• If full batch affordable, try out L-BFGS

1. Lecture(youtube) and PDF ↩