CS231N Lec. 6 | Training Neural Networks I

24 Oct 2020 in Studies on Lecture-Review

please find lecture reference from here¹

CS231N Lec. 6 | Training Neural Networks I

Let’s begin to learn ..

1. One time setup
   activation functions, preprocessing, weight
   initializing, regularization, gradient checking
2. Training dynamics
   babysitting the learning process,
   parameter updates, hyperparameter optimization
3. Evaluation
   model ensembles

Part 1

• Activation functions
• Data Preprocessing
• Weight Initialization
• Batch Normalization
• Babysitting the Learning Process
• Hyperparameter Optimization

---

1. Activation functions

at any of certain layer, inputs comes in and multiplied by some weight(w_i, plus bias)
and then activate it by some of functions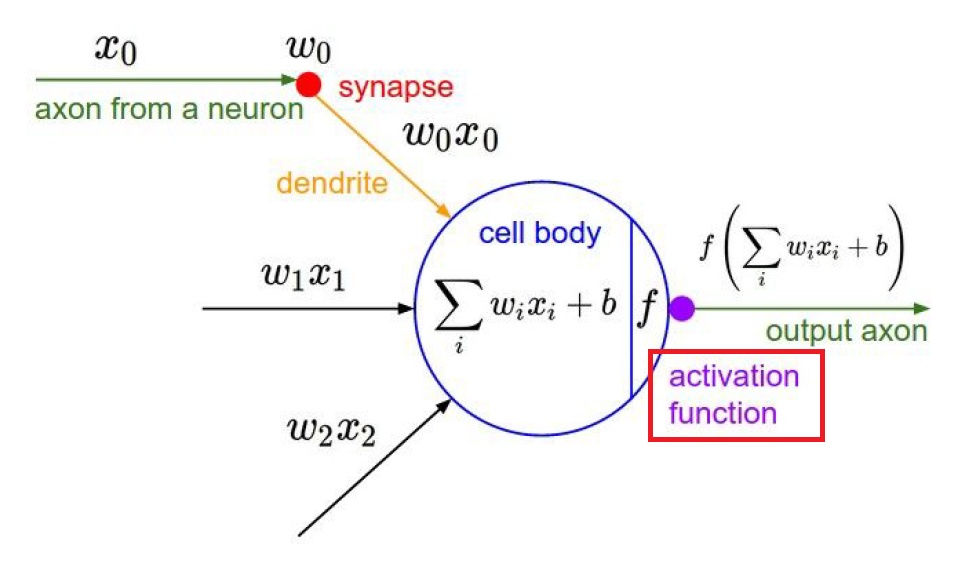

the functions are..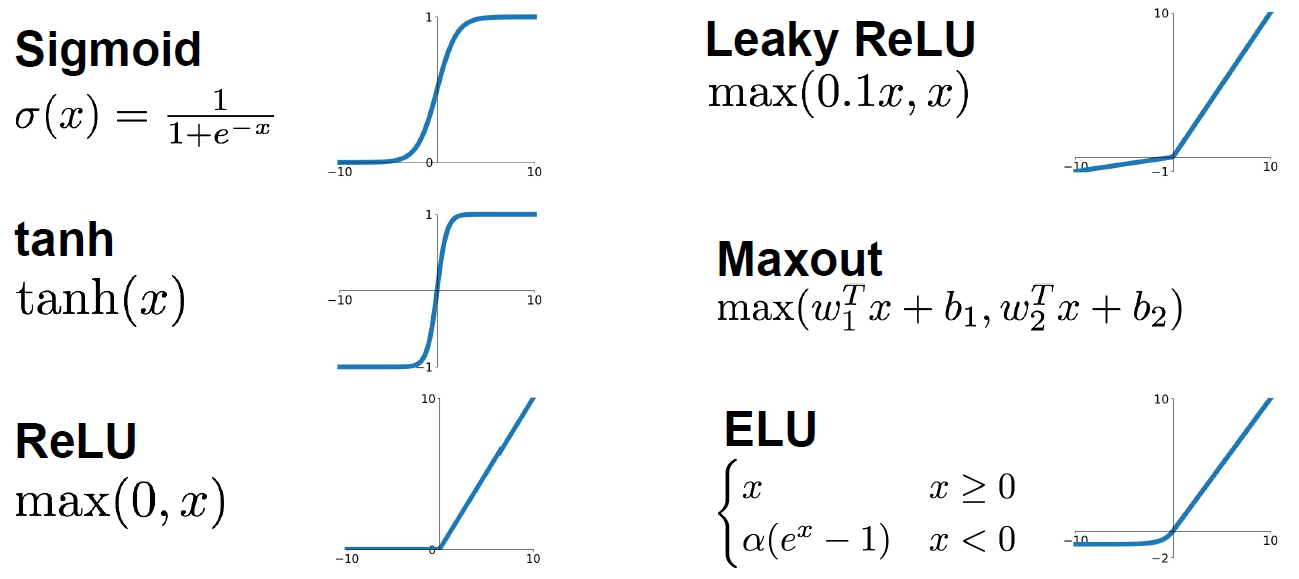

Sigmoid

Output always returns [0,1].
Historically popular, since it have nice performance of saturating value.
But have this have 3 known Problems

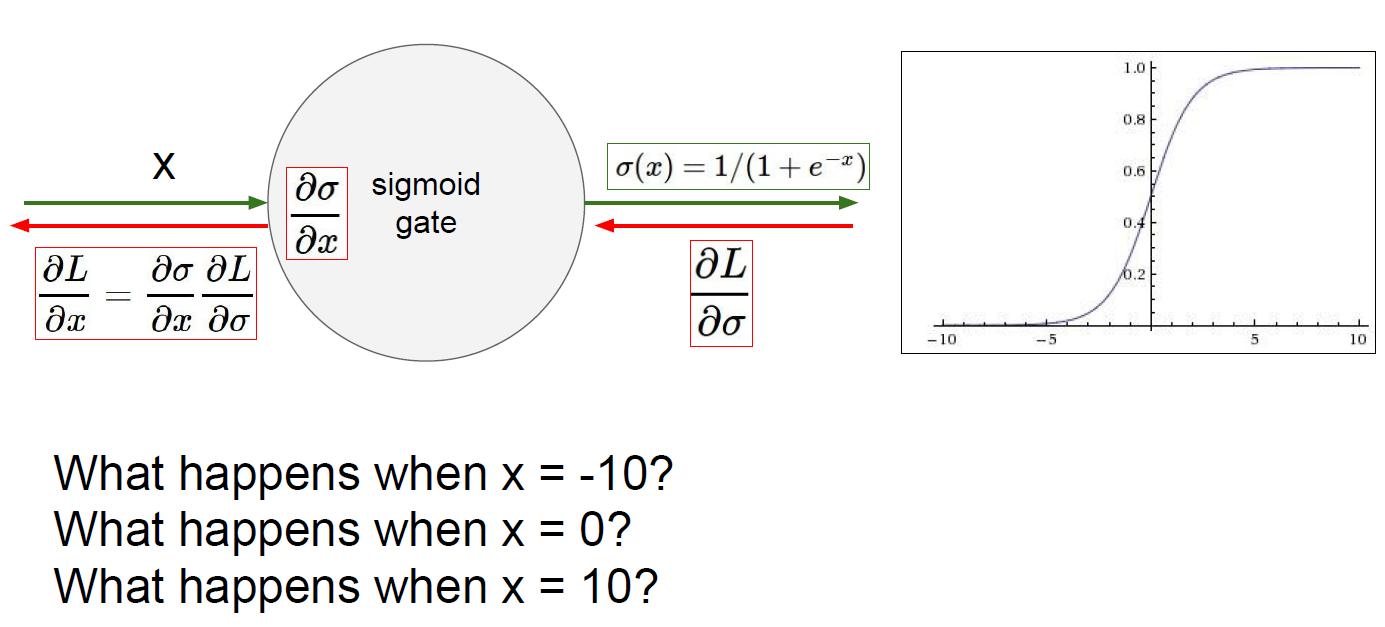
Problem 1 - gradient loss

When x = -10, gradient would be 0
When x = 0, gradient would be fine(proper value for neural network..)
When x = 10, gradient would be 0

So, when activation function is “Sigmoid”, then gradient can be lost.

Problem 2 - output is not zero-centered

As above graph, Sigmoid is not zero-centered.
This will cause quite inefficiency.

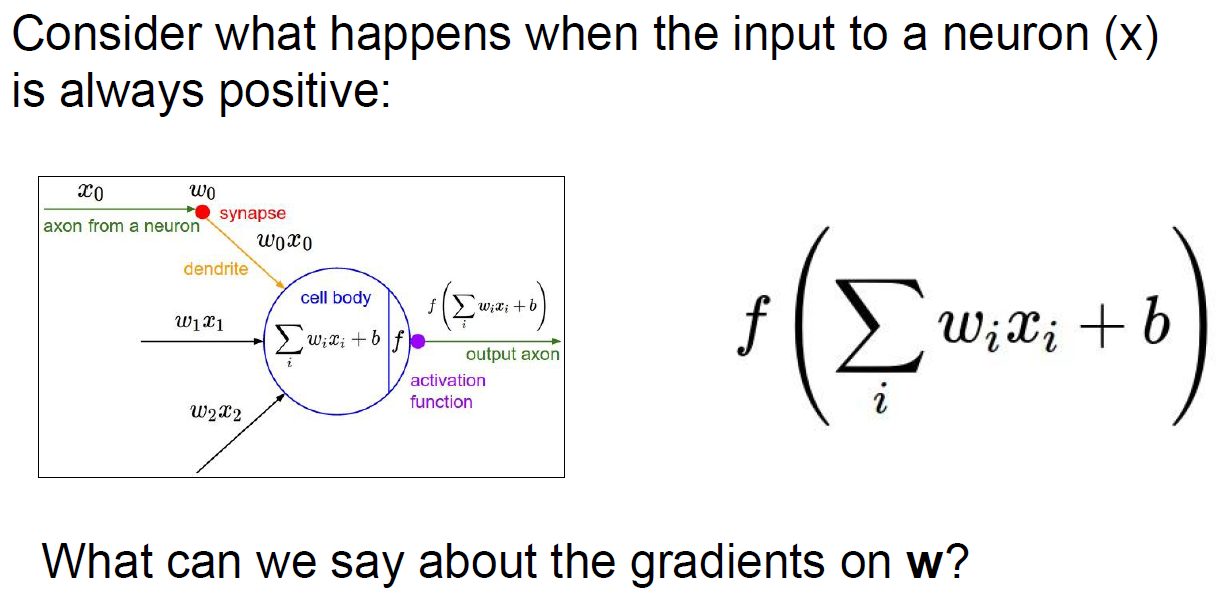
Let’s think of gradient of w.
derivation of sigmoid f is df/dw = x, that is, dL/dw = dL/df(upstream gradient) * df/dw(==x, local gradient).

at this, we assume all x is positive. so, the sign of dL/dw is dependent to dL/df.
it means, sign of gradient is all positive or negative depends on sign of dL/df(upstream gradient).

at below graph, optimal gradient of w is straight forward. But, because of problem2(not zero centered), gradient is going as zig zang path as below.

So, sigmoid could cause inefficiency problem.

Problem 3

It’s quite not main problem, in the grand scheme of network.( conv. and dot-product is dominant )
But it is true that exponential is have computational expensive. ( think of P-NP )

tanh

It’s bit better than sigmoid.
As you can see below figure, this solve zero-centered problem of sigmoid.
But this still kills gradient when saturated.

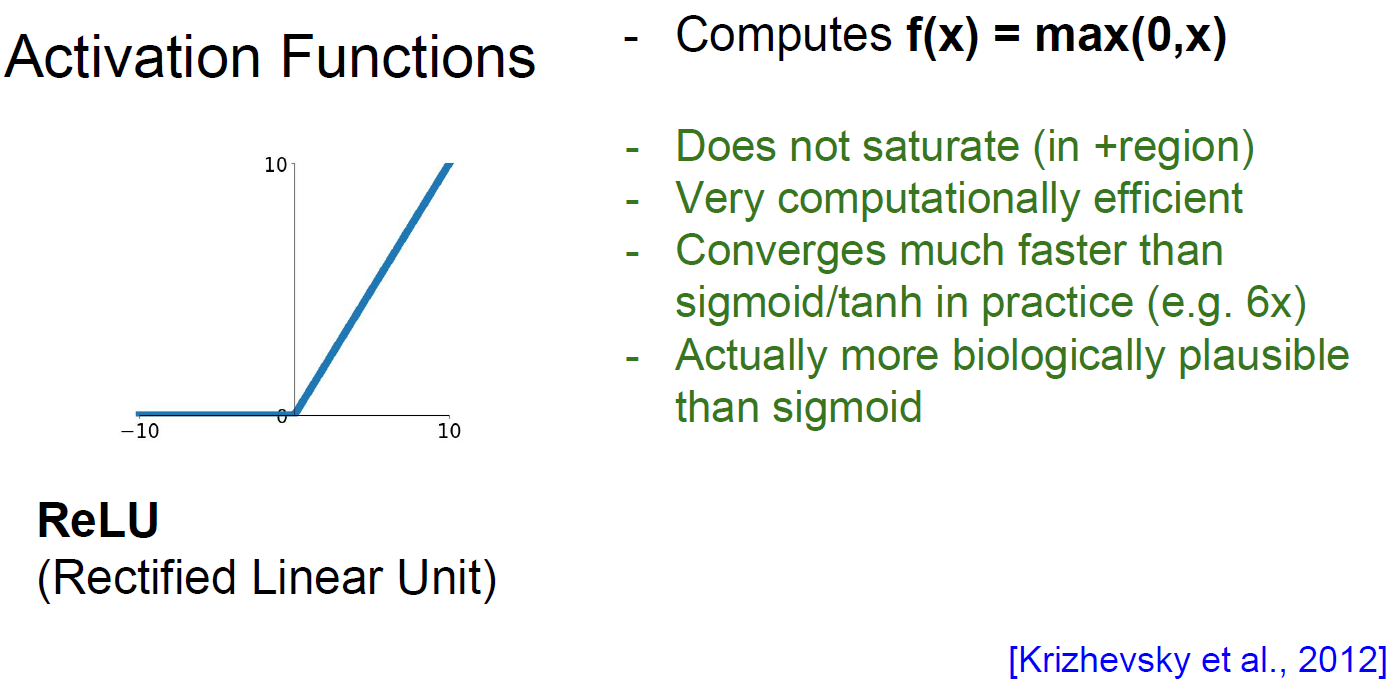
ReLU (Rectified Linear Unit)

This solve many problems observed from sigmoid/tanh.

• Not saturated ( in positive region )
• Much computational efficient. ( linear )
• Converges much faster than sigmoid/tanh in practice ( e.g. 6x )
• More biologically plausible than sigmoid/tanh ( cuz we’re mimicking neuron )

Alexnet, which used ReLU, is major CNN algorithm which could do well on ImageNet and larget-scale data.

But this still have 2 problems,

• Not zero-centered
• An annoyance ( still saturated at negative region)

So, with below two cases, “Dead ReLU” can be increased.

• bad initialization
• learning rate is too high

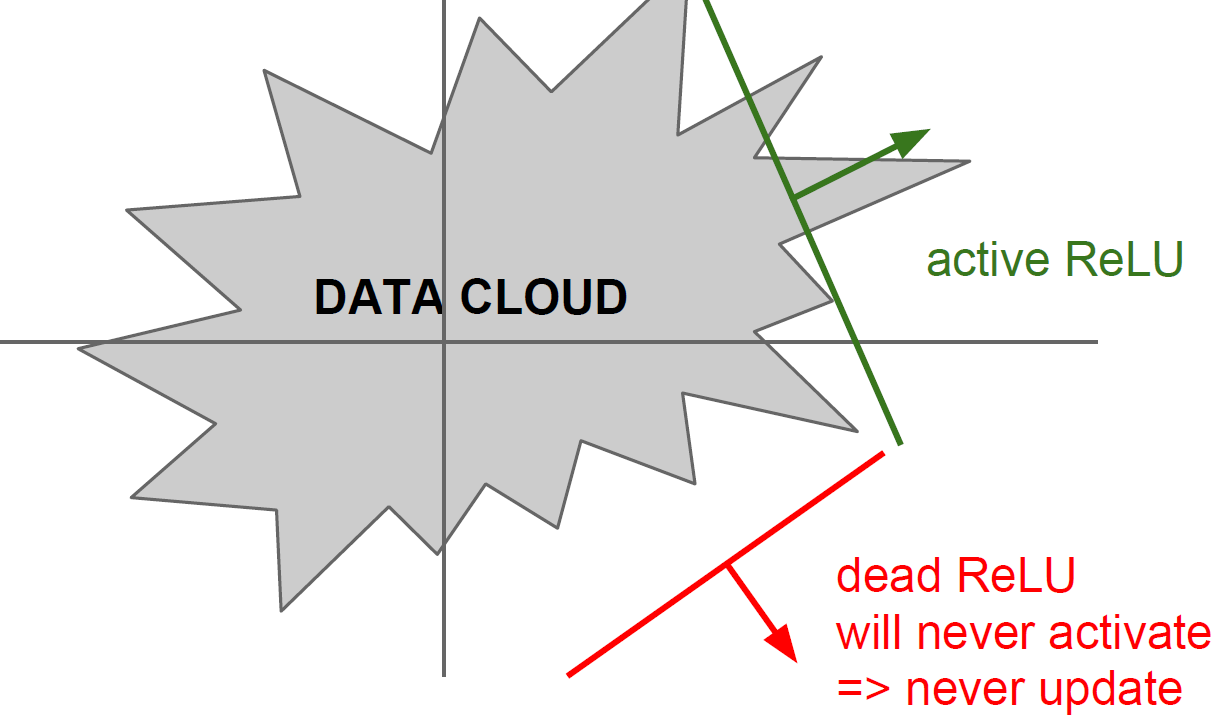
People like to initialize ReLU neurons with slightly positive biases (e.g. 0.01) Not all use, but people use to increase likihood of it being active on beginning.

Leaky ReLU

With simple revision, saturation problem of ReLU can be solved by below two ReLU.

ELU

Another revision of ReLU. This use exponential at negative regime.
So, This could adds some robustness to noise. But Computation requires exp.

Maxout “Neuron”

Not saturated. Abandone linearity and get generalized ReLU and Leaky ReLU.
But doubles # of param./neuron.

TLDR (Too Long Didn’t Read).. In practice,

• Use ReLU(but be careful with your learning rate)
• Try Leaky ReLU / Maxout / ELU
• Try tanh, but don’t expect much
• DON’T USE sigmoid

---

2. Data Preprocessing

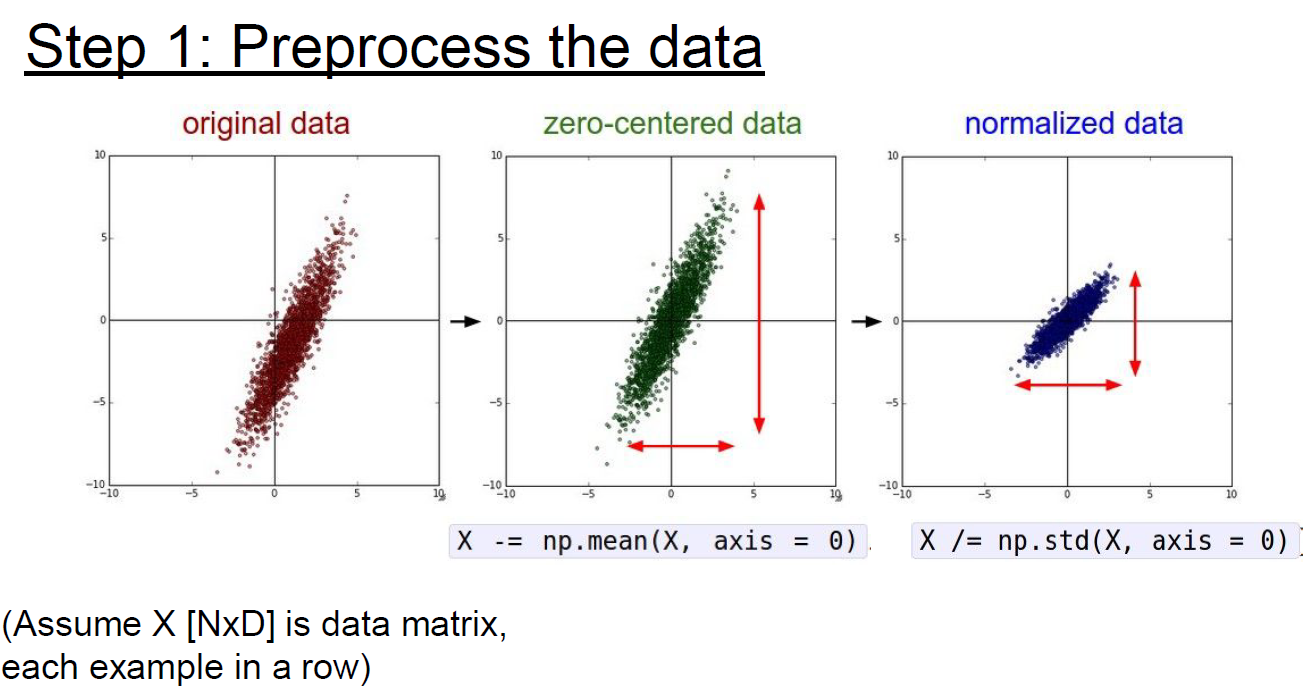
Preprocessing the data

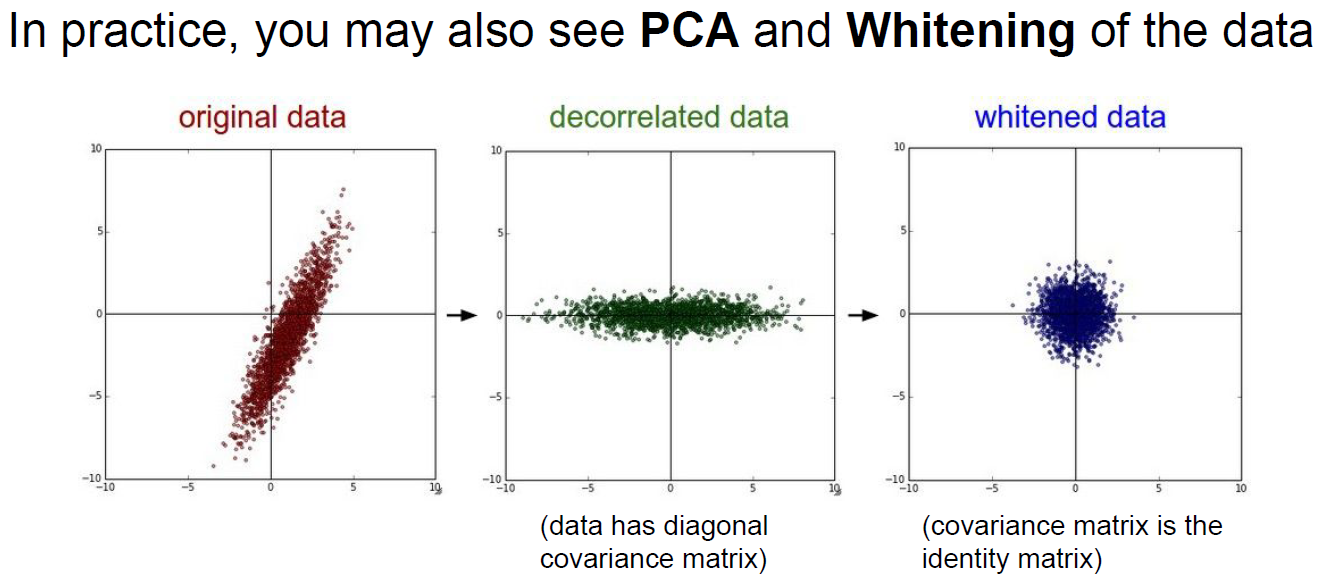
With below preprocessing(zero-centered, normalize, PCA, Whitening), It’s good to get better performance.
But typically, only zero-centered used, to get general performance for images.

Actually, images are already normalized by RGB(0~255). So, don’t doing additional normalization.

Q. Do preprocessing is started once we start learning, not doing per batch?
A. Yes. After enough good batches, then could get good estimate of mean. (even though not training entire data)

Q. Does this zero-centered pre-processing solve sigmoid problem from not-zero-centered?
A. Nope, just only first layer only solved. Not sufficient to further deep learning.

3. Weight Initialization

Let’s assume all W init. as 0.
All neurons will doing same thing and update as samely. Which is what we don’t want. ( each neurons are different based on which class it was connected to, but when looking in all neural network, it going to be same.)

1. Small random number

Good for only small. But for deeper case, all activations become zero.

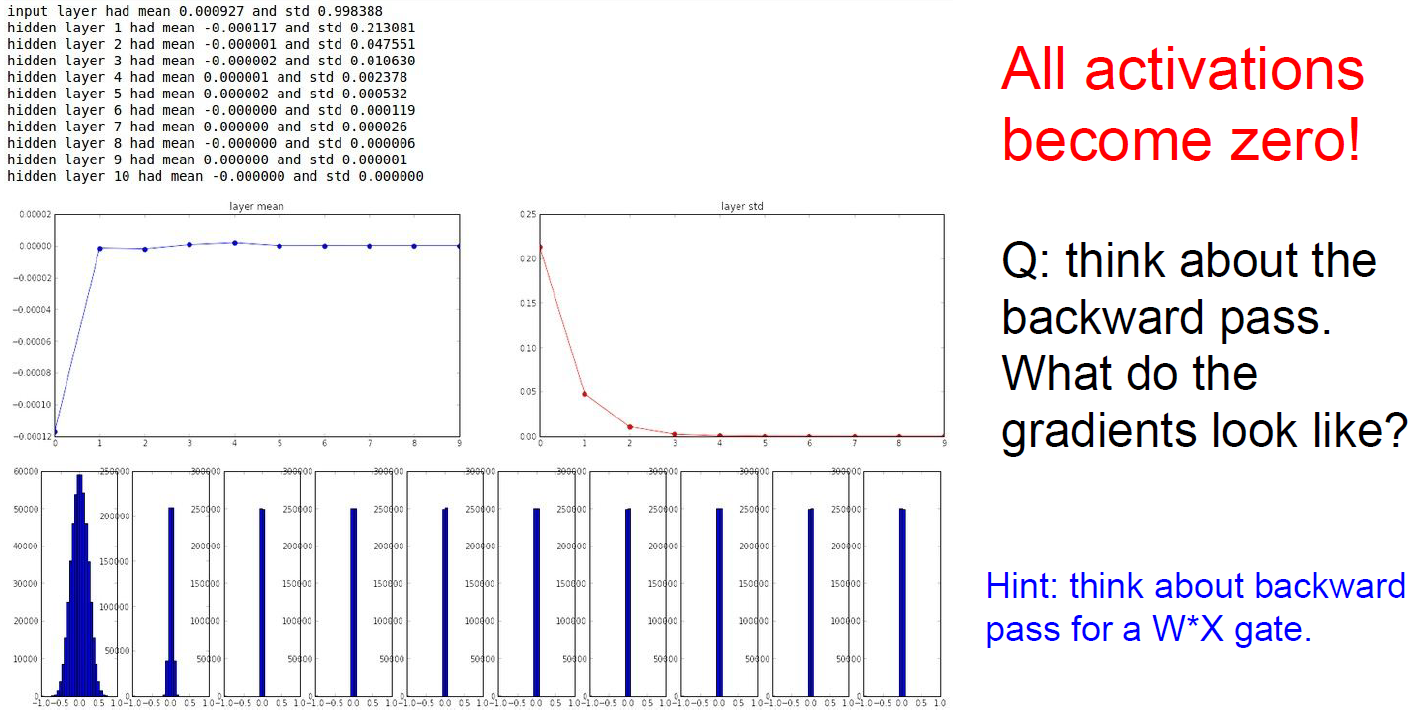
in case of 100times bigger then 0.01, then becomes saturated either 1 and -1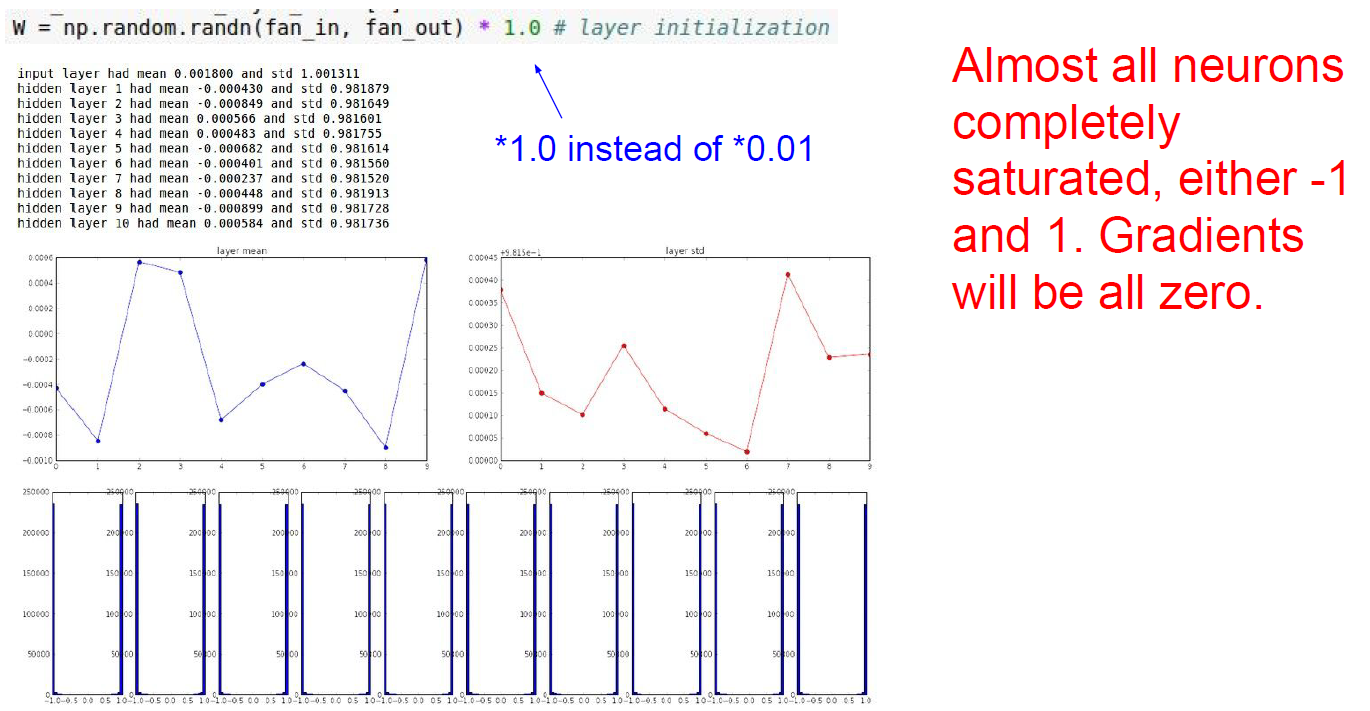

Xaiver Initialization

Good for linear case.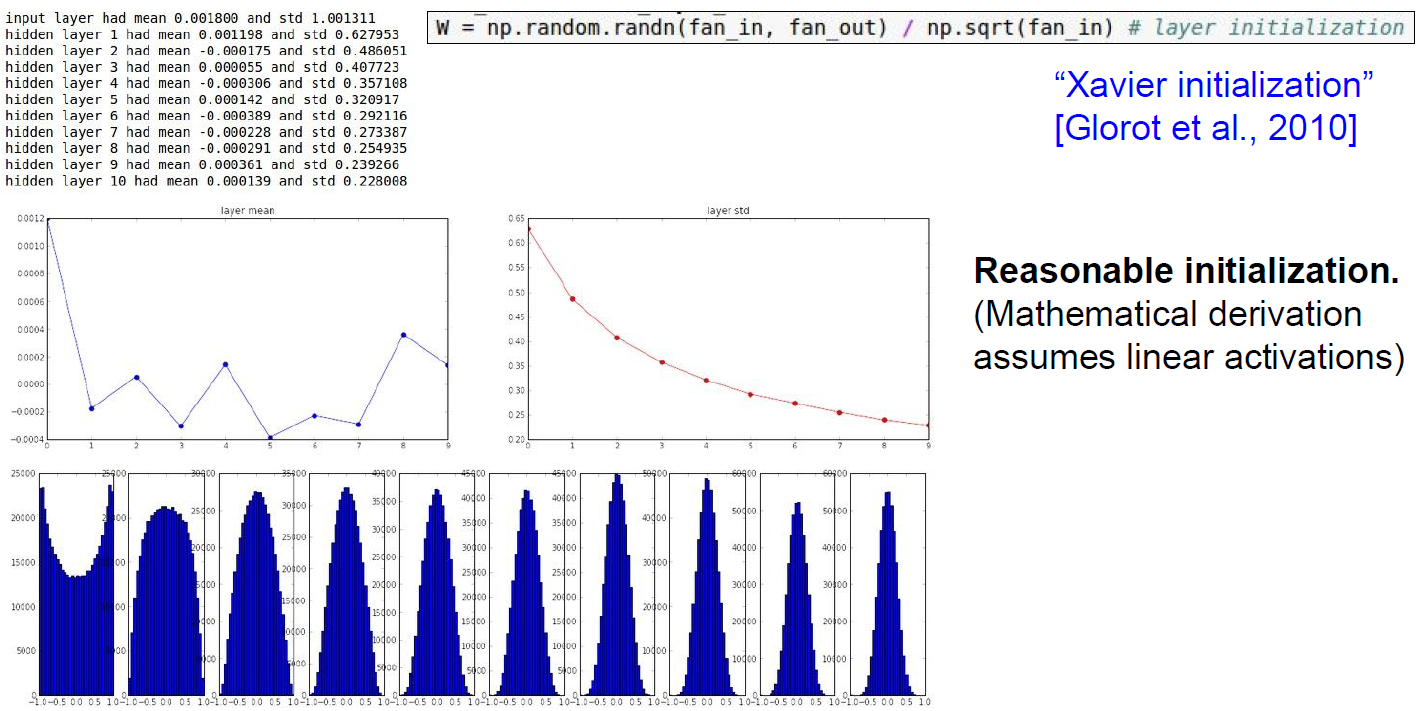

But bad for nonlinear case. (ReLU)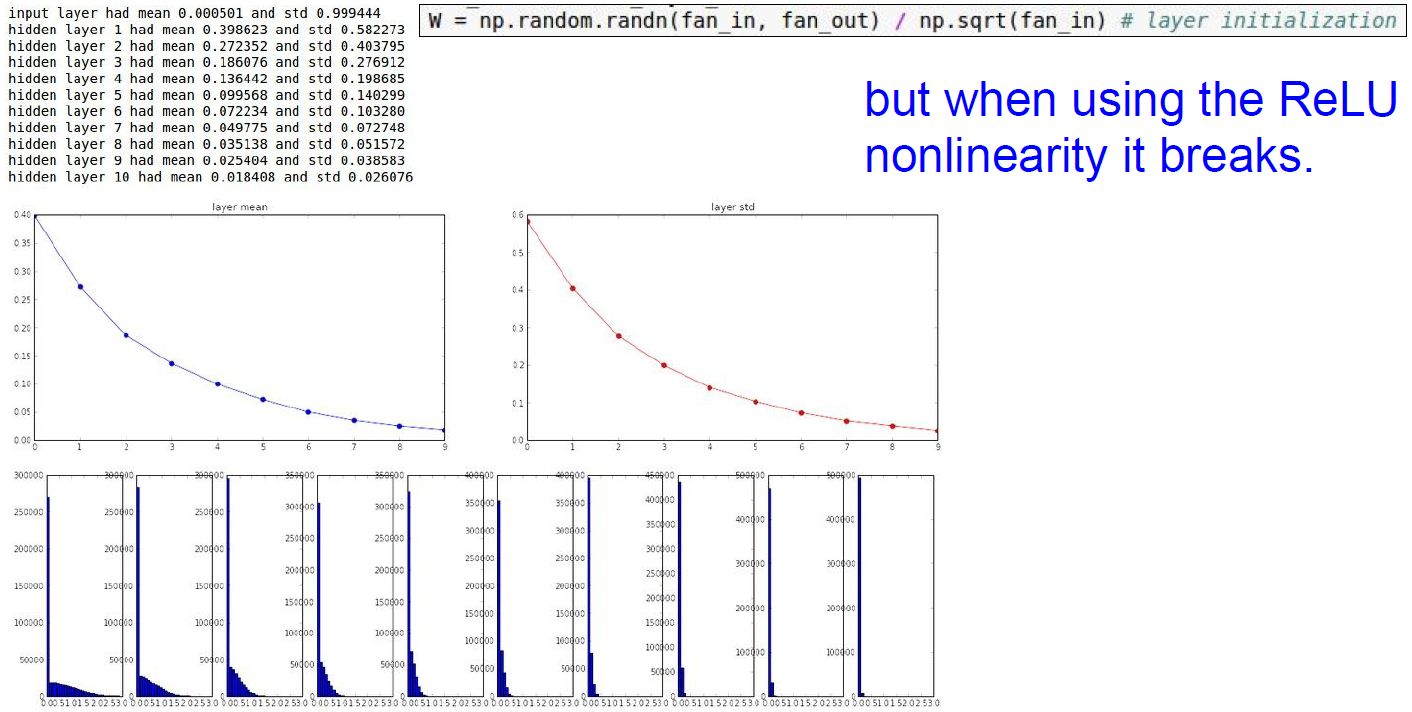

But! can be improved by additional /2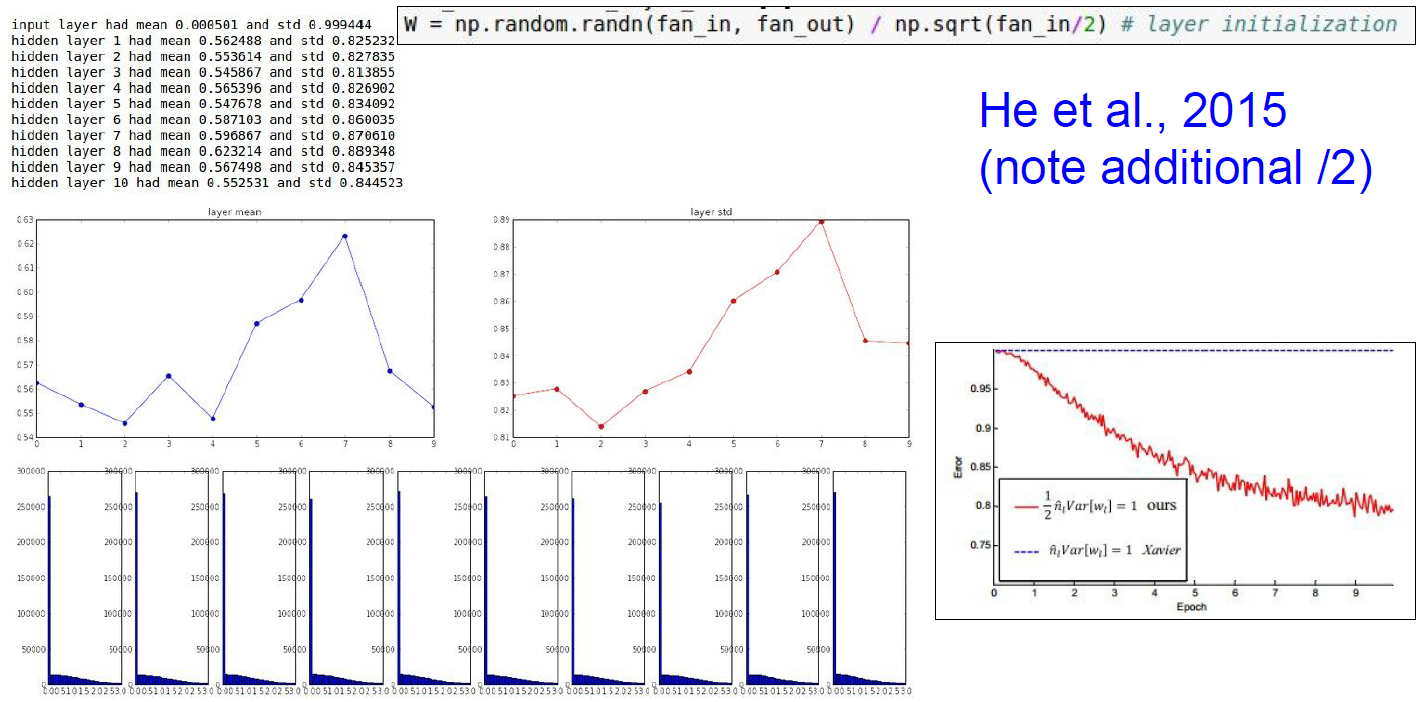

Many researchers are studying for good initializing. Plz refer to belows..

- Understanding the difficulty of training deep feedforward neural networks by Glorot and Bengio, 2010  
- Exact solutions to the nonlinear dynamics of learning in deep linear neural networks by Saxe et al, - 2013  
- Random walk initialization for training very deep feedforward networks by Sussillo and Abbott, 2014  
- Delving deep into rectifiers: Surpassing human-level performance on ImageNet classification by He et al., 2015  
- Data-dependent Initializations of Convolutional Neural Networks by Krähenbühl et al., 2015  
- All you need is a good init, Mishkin and Matas, 2015  

A good general rule of thumb is basically use the Xaiver Initialization to start with, and think of others.

4. Batch Normalization

Recommend to read this paper

BN is a idea to preventing Gradient vanashing.
Training samples : N Dimension : D

Usually inserted after Fully connected or Convolutional layers and before nonlinearity.

Q. Do we necessarily want a unit gaussian input to a tanh layer? A. In point of controlling “how to saturated”, yes. After normalized, network can squash the range by learning.
Both gamma and beta is param. to be learned, gamma is scaling and beta is shifting. These are used for giving flexibility to how BN works. In tanh example, by learning network can choose how to be saturated.

Summary of BN.

• Good gradient flow
• Allow higher learning rate
• Reduce dependency of initialization
• Slightly reduces the needs for dropout.

Q. Do BN could good for small batch size case like reinforcement?
A. Usually no, but have same effects, commonly good.

Q. Do BN change structure?
A. No, it just scaling and shifting.

Q. Does BN could be redundant by recovering identify mapping ?
A. In practice, no. Not learning same as identify mapping.

Q. Does BN make gaussian ?
A. No, it’s approximate values.

Batch Norm. is computed at training time(like running average) and used at testing time.

5. Babysitting the Learning Process

Double check that the loss is reasonable.

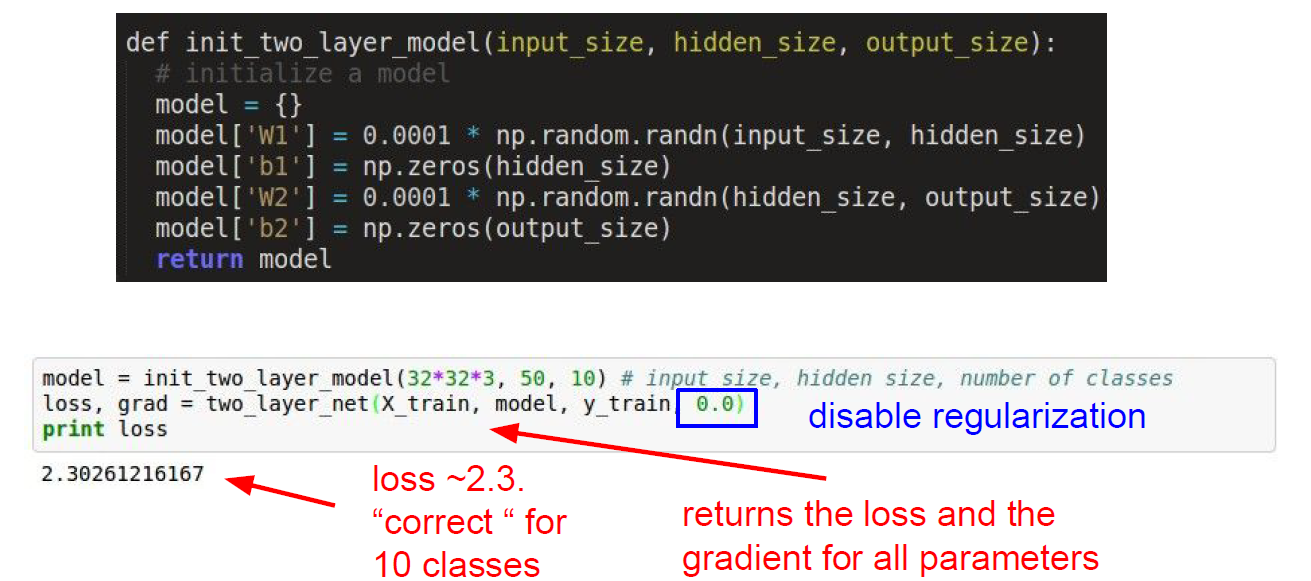sanity check, checking model works as when designed.

Trial for small samples to overfit.

Let’s begin with regularization.
Loss barely changing, cuz learning rate is probably too low.
But it is training.

Let’s change learning rate bigger. 1e6.. super big..
returns NaN, meaning cost exploded.

Rough ranger for learning is [1e-3, 1e-5].

6. Hyperparameter Optimization

How to pick best hyperparameters?

Try cross-validation

• with few epoches to get rough idea.
• longer running time, finer search.
  … repeat

if cost is over > 3*original cost, then break out.

Example for searching hyperparam. it’s good to use log scale value.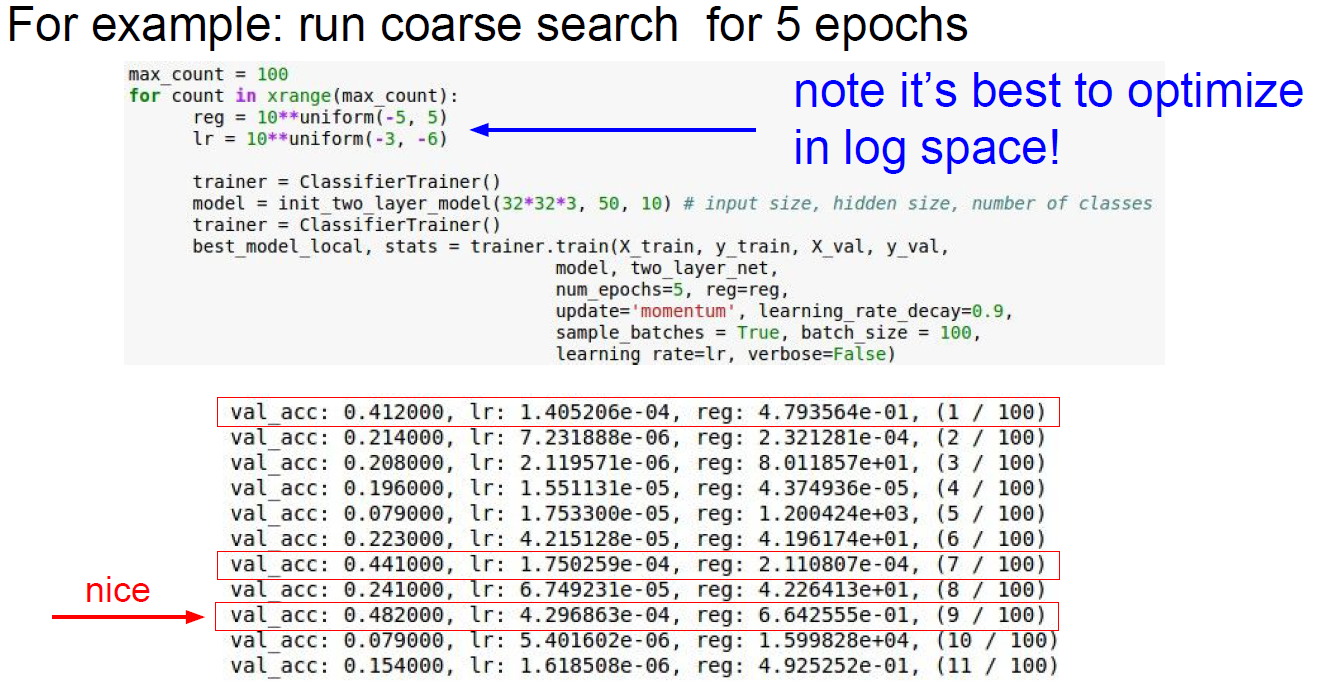

Adjusting and observe reulsts… All learning rate is saturated at e-04, which means better lr could be exist less then e-04.

How to search..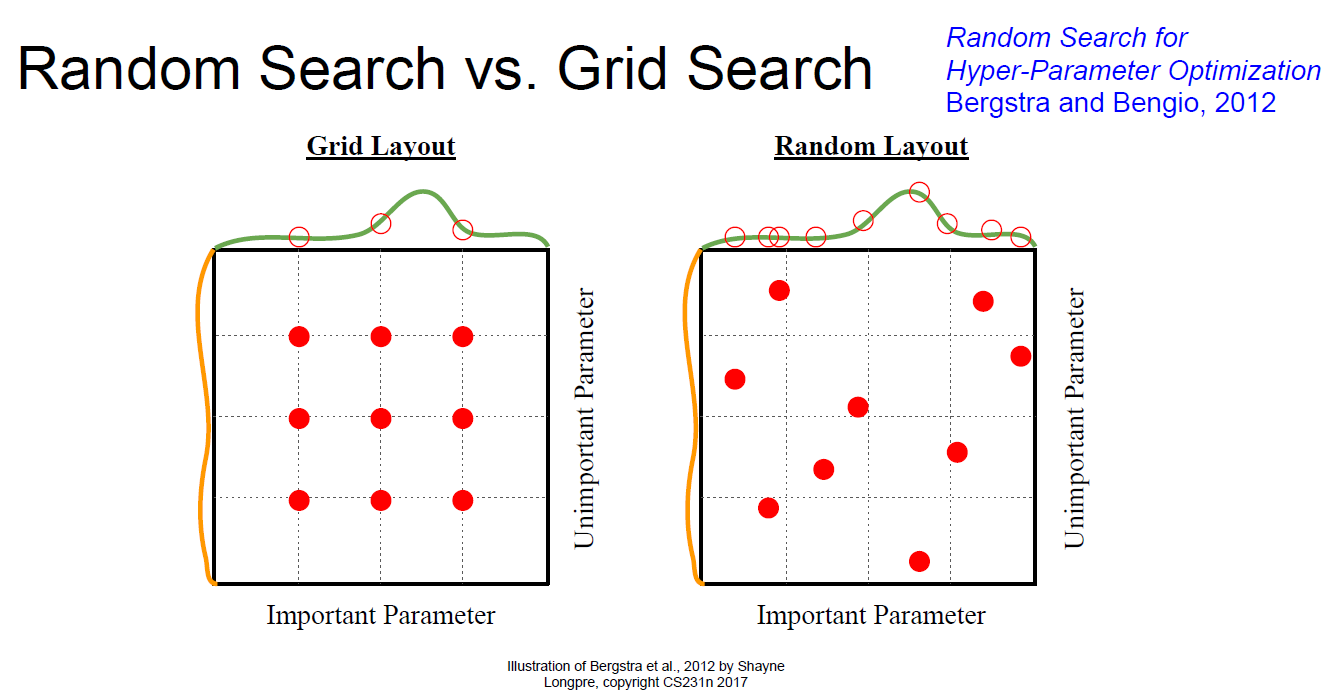

Learning rate samples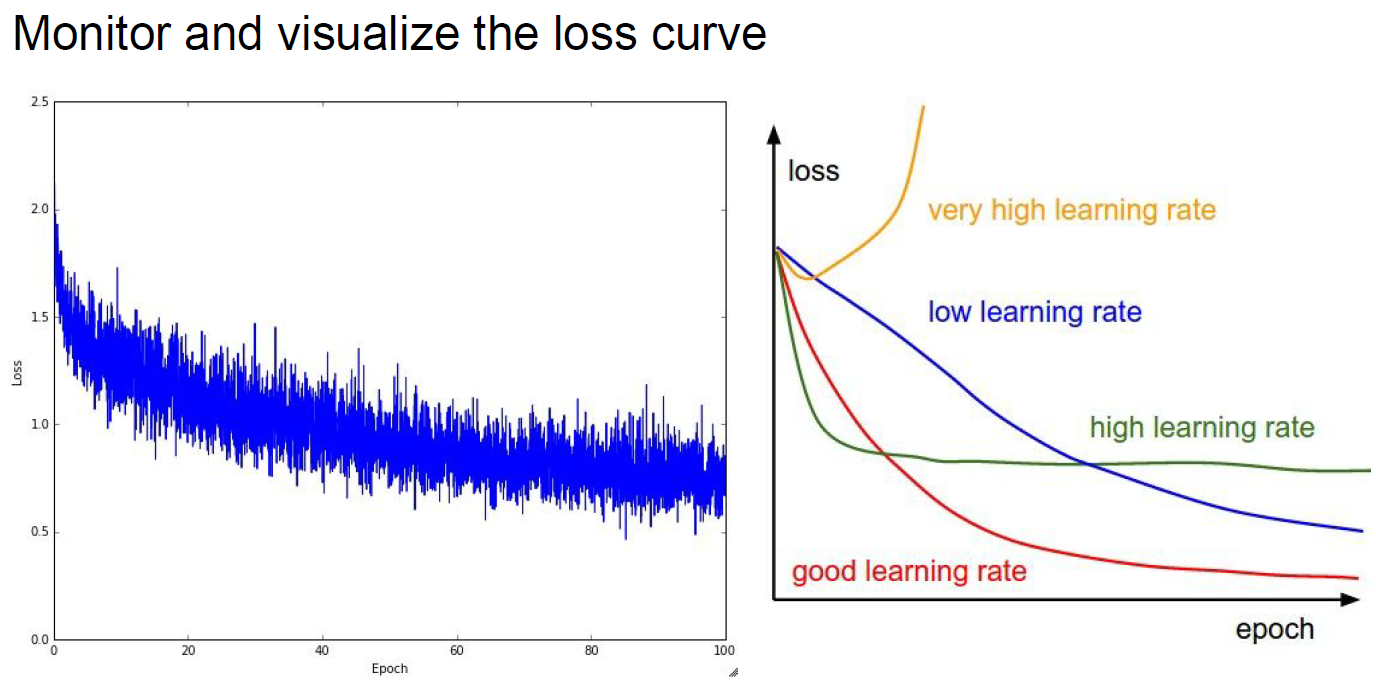

Interpreting Loss graph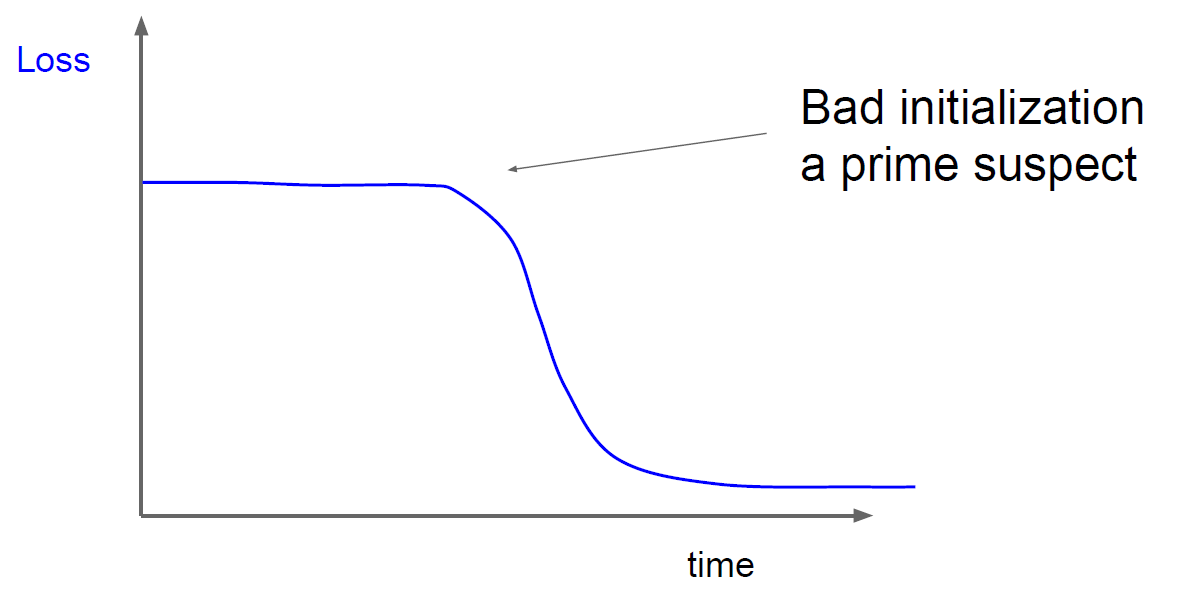

Monitoring accuracy.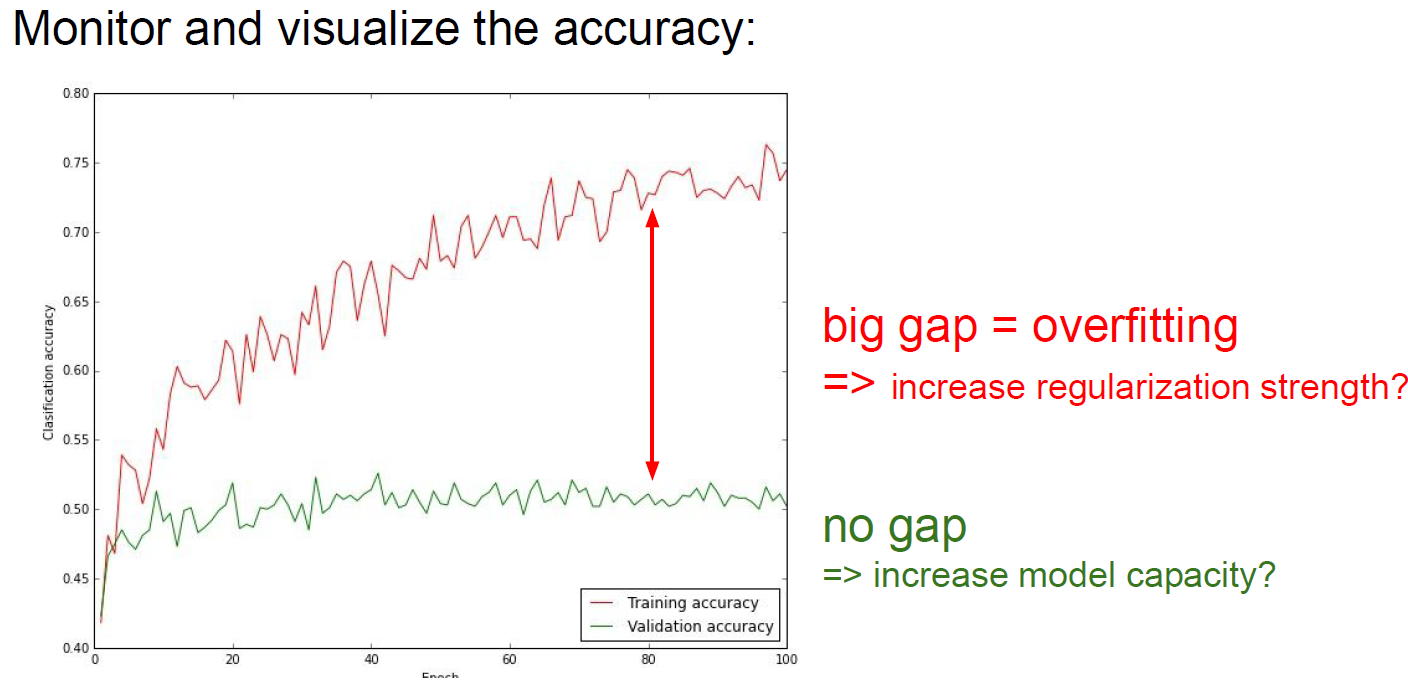

Tracking W diff.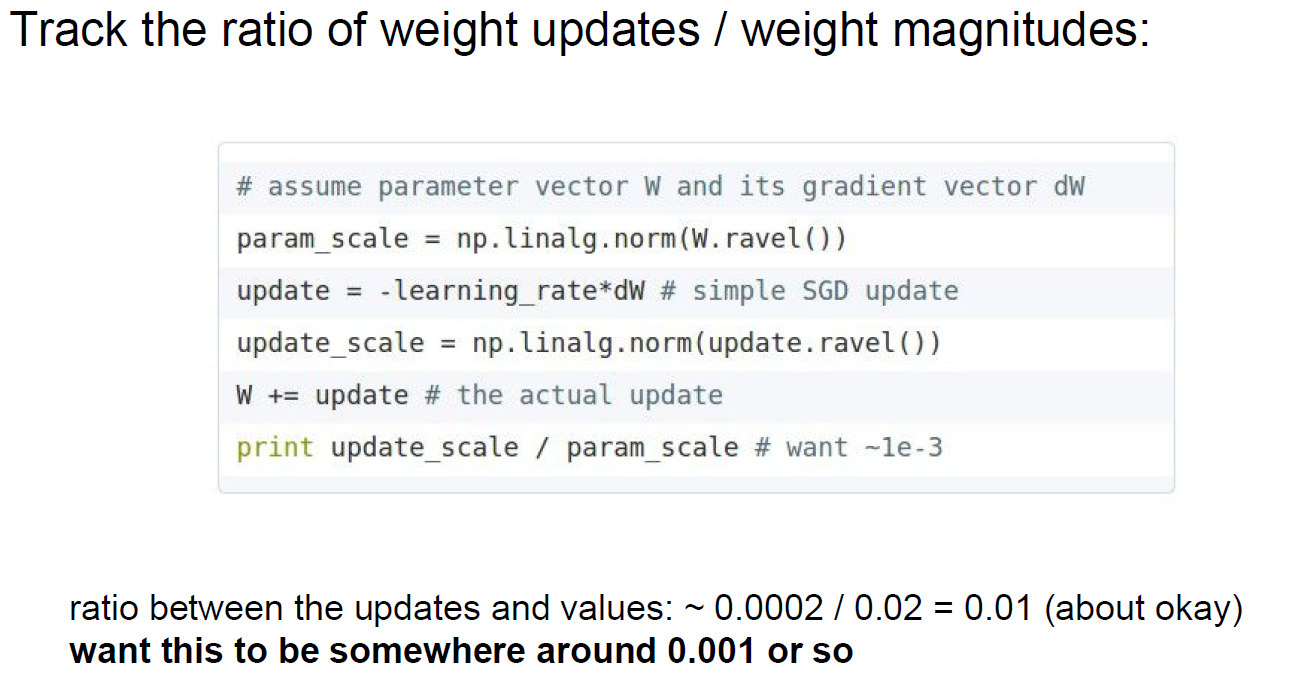

TLDR : Summary

• Activation Functions (use ReLU)
• Data Preprocessing (images: subtract mean)
• Weight Initialization (use Xavier init)
• Batch Normalization (use)
• Babysitting the Learning process
• Hyperparameter Optimization (random sample hyperparams, in log space when appropriate)

1. Lecture(youtube) and PDF ↩